Pendulum Fisik

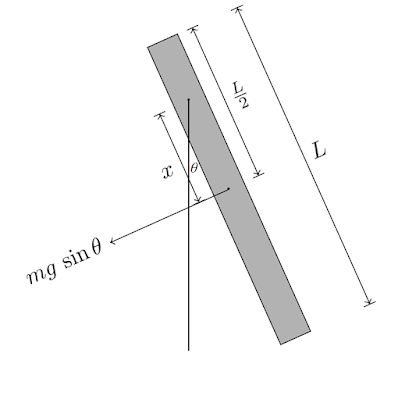
Pendulum fisik adalah sistem pendulum yang terdiri atas benda tegar.  Dalam gambar di atas, batang bermassa $m$ berayun dengan sumbu putar sejauh $x$ dari titik pusat massa. Gaya berat $mg\,\sin\theta$ bekerja sebagai gaya penyebab ayunan.

Momen inersia $I$ dihitung melalui teorema sumbu sejajar.
$$\begin{align*} I = \frac{1}{12}mL^2 + mx^2 \end{align*}$$
Torsi $\tau$ yang bekerja yaitu
$$\tau = -mgx\,\sin\theta$$
Dalam sistem tersebut berlaku
$$\begin{align*} \sum \tau &= I\alpha \\ -mgx\,\sin\theta &= \left( \frac{1}{12}mL^2 + mx^2 \right)\alpha \\ \left( \frac{1}{12}mL^2 + mx^2 \right)\alpha + mgx\,\sin\theta &= 0 \\ \left( \frac{1}{12}L^2 + x^2 \right)\theta '' + gx\,\theta &= 0 \end{align*}$$
Persamaan tersebut adalah persamaan diferensial orde dua. Solusi dari persamaan tersebut adalah
$$\theta(t) = \theta_0 \cos(\omega t)$$
dengan $\omega = 2\pi/T$, dan periode $T$ adalah fungsi dari $x$ dan $L$.
$$T(x,L) = 2\pi \sqrt{ \frac{ \frac{1}{12}L^2 + x^2 }{gx} }$$



Dari grafik tersebut, dapat dilihat bahwa terdapat daerah di mana dua nilai $x$ yang berbeda dapat memiliki nilai periode yang sama. (Kurva di sebelah kanan garis tegak paling kanan tidak berarti, karena di daerah itu $x > L/2$, saat titik tumpu di luar batang)

Periode saat batang diayunkan di ujungnya $(x = L/2)$ sebesar
$$T_{ujung} = 2\pi\sqrt{ \frac{2L}{3g} }$$
Periode yang sama juga didapat saat $x = L/6$. Sedangkan periode minimum sebesar
$$T_{min} = 2\pi \sqrt{ \frac{L}{g\sqrt{3}} }$$
dicapai saat $x = L/\sqrt{12}$.

Saat $x$ menuju nol, periode menuju takhingga. Ini berarti jika sumbu ayunan berada pada titik pusat massa, batang tidak akan berayun, melainkan bergerak melingkar beraturan.